
In this case the outside function is the exponent of 50 and the inside function is all the stuff on the inside of the parenthesis. It looks like the outside function is the sine and the inside function is 3x2+x.
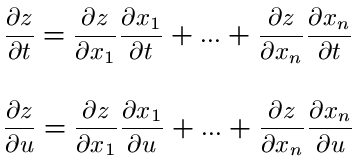
Let’s take a look at some examples of the Chain Rule.Įxample 2 Differentiate each of the following. The outside function will always be the last operation you would perform if you were going to evaluate the function. The square root is the last operation that we perform in the evaluation and this is also the outside function. For instance in the R(z) case if we were to ask ourselves what R(2) is we would first evaluate the stuff under the radical and then finally take the square root of this result. We can always identify the “outside function” in the examples below by asking ourselves how we would evaluate the function. We then differentiate the outside function leaving the inside function alone and multiply all of this by the derivative of the inside function. We identify the “inside function” and the “outside function”. In general, this is how we think of the chain rule. The outside function is the square root or the exponent of 1/2 depending on how you want to think of it and the inside function is the stuff that we’re taking the square root of or raising to the 1/2, again depending on how you want to look at it. This function has an “inside function” and an “outside function”. Let’s take the function from the previous example and rewrite it slightly. That can get a little complicated and in fact obscures the fact that there is a quick and easy way of remembering the chain rule that doesn’t require us to think in terms of function composition. In general, we don’t really do all the composition stuff in using the Chain Rule. We’ve already identified the two functions that we needed for the composition, but let’s write them back down anyway and take their derivatives.Īnd this is what we got using the definition of the derivative. Now, let’s go back and use the Chain Rule on the function that we used when we opened this section.Įxample 1 Use the Chain Rule to differentiate To see the proof of the Chain Rule see the Proof of Various Derivative Formulas section of the Extras chapter. If we have y = f(u) and u = g(x) then the derivative of y isĮach of these forms have their uses, however we will work mostly with the first form in this class. If we define F(x) = (f∘g) (x) then the derivative of F(x) is,Ģ. Suppose that we have two functions f(x) and g(x) and they are both differentiable.ġ. Then we can write the function as a composition.Īnd it turns out that it’s actually fairly simple to differentiate a function composition using the Chain Rule. Let’s keep looking at this function and note that if we define,

So, the power rule alone simply won’t work to get the derivative here. Which is not the derivative that we computed using the definition. If we were to just use the power rule on this we would get, Back in the section on the definition of the derivative we actually used the definition to compute this derivative. None of our rules will work on these functions and yet some of these functions are closer to the derivatives that we’re liable to run into than the functions in the first set.

These are all fairly simple functions in that wherever the variable appears it is by itself. However, if you look back they have all been functions similar to the following kinds of functions.

You must use the Chain rule to find the derivative of any function that is comprised of one function inside of another function.We’ve taken a lot of derivatives over the course of the last few sections.


 0 kommentar(er)
0 kommentar(er)
